Trigonometry is one of the most important branch of mathematics.
The word trigonometry comes from the Greek words trigonon means “triangle” and metron means “to measure“.
Trigonometry is the study of the relation between the sides and angles of a right-angled triangle.
It helps in the calculation of the unknown dimensions of a right-angled triangle using formulas and identities based on this relationship.
Table of Contents
Definition
Trigonometry is the branch of mathematics that deals with the relationship between ratios of the sides of a right-angled triangle with its angles.
Who is father of trigonometry?
Hipparchus of Nicaea (190-120 B.C) a Greek astronomer, mathematician and geographer. He is considered to be “the father of trigonometry“.
He created the first to construct a table of values for a trigonometric function and solved several problems of spherical trigonometry by representing the corresponding values of arc and chord for a series of angles such as 0°, 30°, 45°, 60° and 90°, etc.
Trigonometry Ratios-Sine, Cosine, Tangent
Trigonometric Ratios: Sine, Cosine, Tangent
Trigonometric ratios, also known as trigonometric functions, encompass sine (sin), cosine (cos), and tangent (tan). In a right-angled triangle, with the longest side termed as the hypotenuse, the sides opposite and adjacent to the hypotenuse are crucial.
- Sine (sin): Ratio of the length of the side opposite the angle to the hypotenuse.
- Cosine (cos): Ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan): Ratio of the length of the side opposite the angle to the adjacent side.
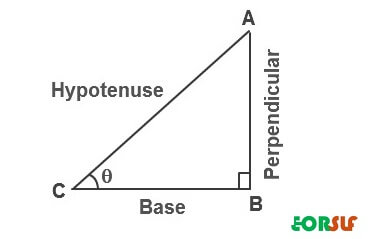
Six Essential Trigonometric Functions
The six fundamental trigonometric functions (trigonometric ratios) are determined by the following formulas, crucial for understanding the sides of a right triangle as depicted in the figure above.
| Function | Abbreviation | Relationship to sides of a right triangle |
|---|---|---|
| Sine Function | sin | Opposite side / Hypotenuse |
| Tangent Function | tan | Opposite side / Adjacent side |
| Cosine Function | cos | Adjacent side / Hypotenuse |
| Cosecant Function | cosec | Hypotenuse / Opposite side |
| Secant Function | sec | Hypotenuse / Adjacent side |
| Cotangent Function | cot | Adjacent side / Opposite side |
Even and Odd Trigonometric Functions
Trigonometric functions can be categorized as even or odd.
Odd trigonometric functions: A function is odd if f(-x) = -f(x), symmetric about the origin.
Even trigonometric functions: A function is even if f(-x) = f(x), symmetric about the y-axis.
Based on identities:
- Sin (-x) = – Sin x
- Cos (-x) = Cos x
- Tan (-x) = -Tan x
- Csc (-x) = – Csc x
- Sec (-x) = Sec x
- Cot (-x) = -Cot x
Hence, cosine and secant are even functions, while sine, tangent, cosecant, and cotangent are odd functions. Understanding these properties aids in simplifying trigonometric expressions, especially when dealing with negative variables inside the function.
Trigonometry Angles and Ratios
Common trigonometry angles, including 0°, 30°, 45°, 60°, and 90°, facilitate trigonometric problem-solving. The ratios sine, cosine, and tangent for these angles are easily memorable. These ratios are determined with reference to a right-angled triangle, where one acute angle corresponds to the trigonometry angle. Here’s a breakdown:
For instance, in a right-angled triangle,
- Sin θ = Perpendicular/Hypotenuse
- θ = sin⁻¹ (P/H)
- Similarly,
- θ = cos⁻¹ (Base/Hypotenuse)
- θ = tan⁻¹ (Perpendicular/Base)
Trigonometry Table
Trigonometry Table Refer to the table below for the common angles used in solving trigonometric problems:
| Angles | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 |
Know More About; Trigonometry Table | Trigonometric Ratios Table.