Trigonometry is a branch of mathematics that studies the relationship between the ratios of a right-angled triangle’s sides and its angles.
It uses trigonometric ratios to find the angles and missing sides of a right-angled triangle.
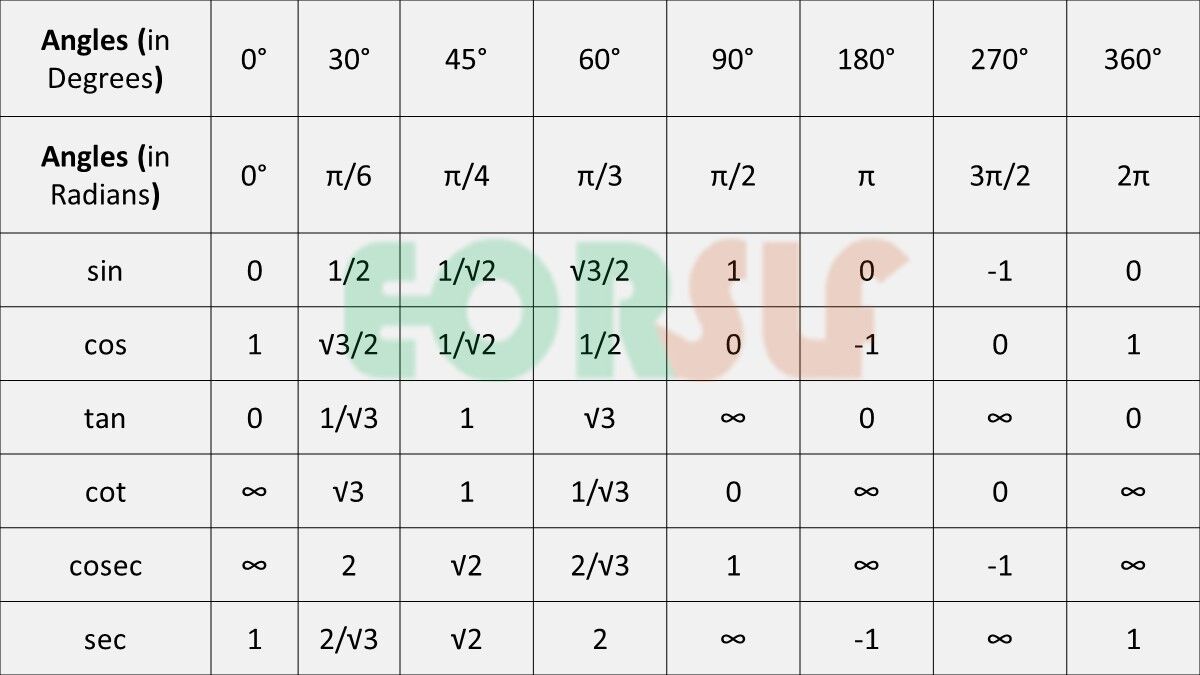
Trigonometry Table
Trigonometric table helps to find the values of trigonometric standard angles angles in degrees and radians, that very easy to convert of degrees in radians and vice versa, radians in degrees.
Its collection of trigonometric values of various standard angles including 0°, 30°, 45°, 60°, 90°, sometimes with other angles such as 180°, 270° and 360° and trigonometric functions – sine, cosine, tangent, coscent, secant, cotangent in a tabular format. These functions can be be written in short as sin, cos, tan, cosec, sec, and cot.
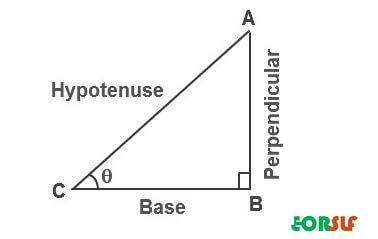
sin = perpendicular / hypotenuse
cos = base / hypotenuse
tan = perpendicular / base
cosec = hypotenuse / perpendicular
Cot = base / perpendicular
Sec = hypotenuse / base
Check the below trigonometry table for trigonometric ratios, trigonometric function values for standard angles and Understand trigonometry table tricks.
Trigonometric Ratios Table
| Angles (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angles (in Radians) | 0° | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
| sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |